A Beginner’s Guide To The Ratio Scale

The ratio scale is a fundamental concept in statistics.

It is commonly used to measure and quantify different types of data. It is an essential tool for beginners, providing the basis for many statistical analyses and data visualizations.

A ratio scale is a measurement scale with a fixed zero point and equal intervals between values. Thus, you can compare and calculate ratios between the notches on this scale. 

For instance, if the ratio between two values is 2:1, one value is twice as large as the other.

Understanding the ratio scale is essential for data analysis or for presenting data meaningfully. It can measure a wide range of data, from weight and height to income and population size.

Once we conclude this guide, you will have a solid understanding of the ratio scale & how to utilize it to measure & compare different data types.

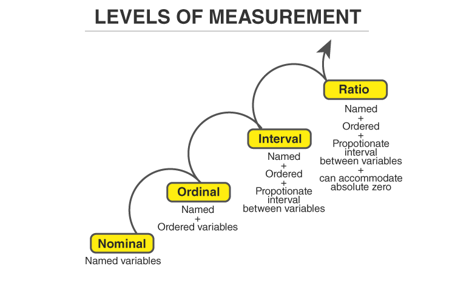
What is the Ratio Scale?

The ratio scale developed by psychologist Stanley Smith Stevens is the highest of the four “levels of measurement.”

The ratio scale is quantitative, and you can think of it as a combination of nominal, ordinal, and interval scales. That said, the scale provides researchers with data containing equal intervals that can be compared and ranked.

What makes the ratio scale unique from the other four scales is the true zero value (aka character of origin). This feature tells the researcher that a variable might have a zero presence on the scale.

The best ratio scale examples are height and weight. The section below mentions some more examples:

Ratio Scale Examples

#1. How much do you weigh in kgs?

• Less than 50 kg
• 51- 70 kg
• 71- 90 kg
• More than 91 kg

#2. How often do you use your smartphone daily?

• Less than 2 hours
• 2-4 hours
• 4-6 hours
• More than 6 hours

#3. How often do you read in a day?

• Less than an hour
• 1-3 hours
• 3-5 hours
• More than hours

Related: Nominal, Interval, Ordinal Scale: A Guide To Measurements & Data Scales

Characteristics of Ratio Scale

The following are the characteristics of the ratio scale: 

1. Has an absolute zero value: You can use the ratio level of measurement to compare and calculate the ratios between two values.
   
2. Allows multiple possibilities for statistical analysis: Using the scale, you can systematically add, subtract, multiply, and divide (ratio) variables. Calculate the mean, mode, median, and chi-square values.
   
3. Do not contain negative numbers: It has no negative values due to its zero point attribute. Hence, to measure any variable, you must verify beforehand that the variable meets all the criteria of the ratio scale.
   
4. Supports unit conversion: The scale supports unit conversion. For example, you can convert units, such as Joules and kilogram calories, to calculate the energy flow.
   
5. Possess characteristics of the other three scales: A ratio scale does everything that an interval, ordinal, and nominal scale does.
   
6. Ratio data can be continuous or discrete: You can represent ratio data using discrete variables (countable values) or continuous variables (infinite values).

How to Measure Ratio Scale?

You can utilize a number of procedures to analyze ratio data. Once you gather the required ratio data, you can collect descriptive & inferential statistics. You can perform almost all of the statistical tests on ratio data.

Descriptive statistics offers you with dataset summary, whereas inferential statistics allows you to compare samples & deduce insights depending on the obtained results.

Here are some of the most common techniques that you may use to interpret ratio data.

Descriptive Statistics For Ratio Data

Here are some common descriptive statistical methods that you can use to analyze the ratio data: 

• Frequency distribution: To get a tabular, graphical, or visual overview of your data
• Mean: To find the sample’s average value
• Median: To find the sample’s central value
• Mode: To find the most commonly appearing value
• Standard Deviation: To quantify the deviation of a dataset from its means (or average) value
• Variance: To calculate the variation in a dataset against the mean
• Range: To calculate the difference between the highest & the lowest values in the dataset

Inferential Statistics

You can analyze ratio data using the following inferential statistics:

• Trend Analysis: To analyze the collected data for trends & insights
• SWOT Inspection: To examine the strengths, opportunities, weaknesses, & threats of a business
• Conjoint Analysis: You can analyze complex decision-making by customers on an interval scale
• Totally Unduplicated Reach and Frequency or TURF Analysis: Allows you to identify the best mix of services, media channels, or products that can reach the largest target audience while minimizing overlap
• Cross-Tabulation: To deduce the relationship between multiple variables

You Might Also Like: Nominal VS Ordinal Scale.

Conclusion

The ratio scale is the highest measurement level. When it comes to pure science, it contains all the aspects that help classify it as a research scale.

The existence of a true zero value is its main selling point. 

Unlike ordinal and interval scales, the ratio scale checks every box regarding magnitude, equal intervals, and ratio values. Thus, making it a great tool for further research and drawing out conclusions.

Hence, it is a great asset for businesses to enhance their services or products.

You may put it to use to understand your clientele better, thereby enhancing your business.

Register with SurveyPoint, create the perfect surveys, questionnaires, & quizzes using simple steps, and watch the insights flow in.

Check out our template collection.