Standard deviation and standard error are two important but distinct concepts that researchers and users confuse.
When examining and evaluating data, you look for patterns and insights that can reveal information. You may utilize data, for instance, to learn more about local residents’ spending patterns. In this situation, collecting data from every city resident is not feasible, so you would have to extrapolate your conclusions based on a sample of data. Hence, knowing how close or how precisely the sample data represents the entire population as part of your study is crucial. In other words, how comprehensive is your study?
Statistical concepts such as standard deviation and standard error come into play in such cases. Let’s take a closer look into the definitions of standard deviation and standard error in detail and the differences between the two.
Standard Deviation
Statisticians use the standard deviation as one of their main pillars.
It measures central dispersion and represents the distribution’s spread. Although it can also refer to population variability, “standard deviation” is often used to explain sample distribution variability.
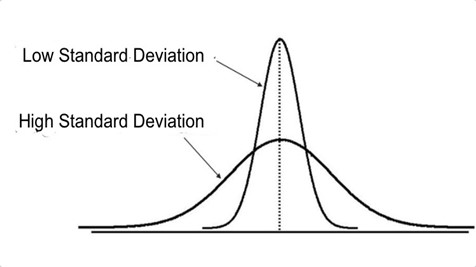
In simple terms, standard deviation shows you how far away each value is from the mean. The standard deviation equals the square root whenever there is a positive variance.
Generally, values falling outside the mean are characterized by a high standard deviation. In contrast, a low standard deviation indicates a clustering of variables closer to the mean.
Calculating the standard deviation
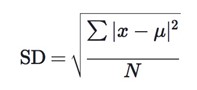
Where:
- x stands for a value in a data set
- ∑ denotes the sum of values
- μ indicates the data set’s mean
- N stands for the number of values in the sample
One must
- Calculate the mean or arithmetic mean of the data
- Calculate the squared deviations from the mean. (Data value – average) 2
- Find the average squared difference. (Variation = The sum of squared differences multiplied by the number of observations)
- Determine the square root of the variation. (Standard deviation = √variance)
Standard Error
Unlike standard deviation, which describes a sample’s dispersion, standard error depicts the sample’s representation of a population.
For estimating population parameters, researchers must first decide the level of accuracy they require or the amount of error they are prepared to tolerate. The term “standard error” also refers to the degree of error, which denotes a discrepancy between sample statistics and the population parameter.
No matter how diligently we try, estimating an unknown population parameter will always be subject to some error. Therefore, when computing population characteristics, it is also necessary to account for standard errors. Rather than a comprehensive census, estimates are based on random samples from the entire population. Hence, standard errors are measures of accuracy.
Another way to think of standard error is as a statistic representing an estimate’s precision. It enables us to compare estimates, like sample means, to population parameters, like population means.
Let’s look at standard errors for mean and proportion by taking a simple one-sample example.
Standard Error for the Mean
As the sample size increases, the standard error of the mean decreases. However, it decreases by a factor of n½, not n. In the case of one sample, the standard error for the mean can be expressed as follows:
s / √ (n)
Where:
- s: represents the standard deviation of a sample
- n: denotes the size of a sample
It is, therefore, not particularly cost-efficient to expand the sample size by fourfold if the researcher wants to minimize the error by 50%. Calculating the difference between means can be done using the following formula:
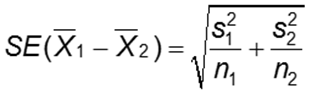
Related: Agile Market Research: A Revolutionary Way To Gain Insight
Standard Error for the Proportion
The standard error of proportion is denoted by p and q (1 – p), representing the probability that an event will occur successfully or unsuccessfully. Moreover, in terms of formulas, it is defined as:
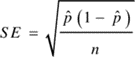
The difference between proportions can be calculated using the formula below:
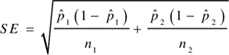
Distinctions Between The Standard Deviation And The Standard Error
As far as the difference between standard deviation is concerned, the following points are significant:
- The metric used to evaluate the degree of variance in a set of observations is called standard deviation. An estimate’s accuracy is assessed by its standard error or the measure of variability in its theoretical distribution.
- A descriptive statistic is the standard deviation, whereas an inferential statistic is the standard error.
- The distribution of observations in relation to the normal curve is called the standard deviation. In contrast, the standard error represents the distribution of an estimate concerning the normal curve.
- The standard deviation is obtained by taking the square root of the variance. We can calculate the standard error by dividing the standard deviation by the sample size.
- A more precise standard deviation measurement is given by increasing the sample size. This contrasts with standard error, which decreases as the sample size increases.
Related: A comparison between Descriptive and Inferential Statistics
Let Us Do The Maths for You
Basic Statistics + Comparative Analysis = Tangible Solutions
Seeing a difference between two numbers is easy, but determining whether that difference is statistically significant takes a little more effort. Especially if your question has several possible answers or you’re comparing findings from different groups of respondents, the process can be tricky.
Don’t refrain from investing in the proper technologies to alleviate the burden of manual analysis. Take the hassle out of the equation and let SurveyPoint do all the heavy lifting for you. Sign Up for FREE Today!
Kultar Singh – Chief Executive Officer, Sambodhi