Systematic Random Sampling: Overview, Advantages, and Disadvantages 

Systematic random sampling is a simple, easy-to-use, extremely effective (and accurate) strategy for zeroing in on a target population to unearth precise information.

Throughout this article, you will learn about systematic random sampling and how you can design random sample surveys to understand a population of interest better.

Probability sampling  

Probability sampling entails utilizing probability theory to pick a population for systematic sample research. In this case, the researcher picks a sample typical of the population whose characteristics they seek to examine. Statistical sampling is used to assess a population’s characteristics based on systematic random sampling. 

Systematic random sampling 

In systematic random sampling, the unit is chosen at random. Following this, a new set of sample units is randomly selected at regular intervals until the necessary number of units is selected. Here are some steps that go into obtaining a systematic random sample:

• To begin, select 1 to N units for your population, 
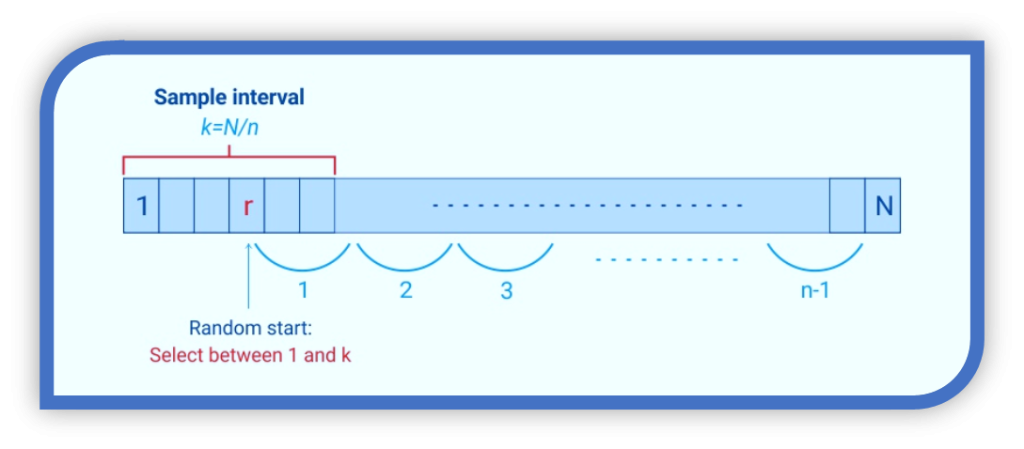
• Decide the n (sample size) you desire or need for your study where i = N/n = the interval size, 
• One can also select one of the integers from 0 to i at random 
• Select every i-th unit. 

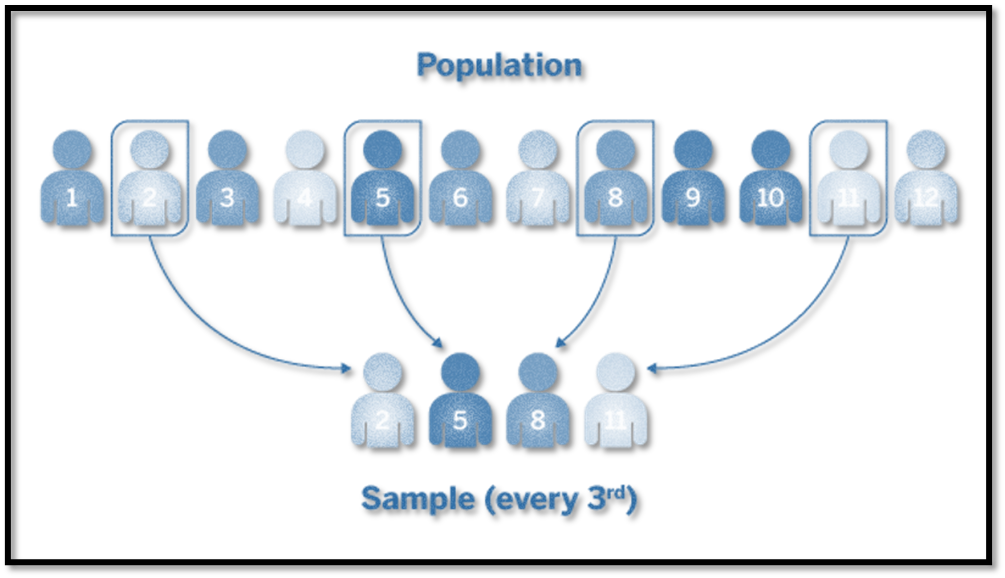
In systematic sampling, the first sample unit is selected, and successive samples are selected based on the previous one. As a result, the potential of an order bias exists. 

In a selection process based on predictability and sample frame lists, the notion of randomness is undermined. Either way, our estimates would be off. However, when the sample frame is arranged randomly, systematic sampling becomes mathematically equivalent to simple random sampling.

As long as the list is segmented based on certain criteria, systematic sampling is the same as segmented sampling. 

Repeated systematic sampling is a kind of systematic sampling that attempts to overcome order biases caused by periodicity or the existence of a pattern in the sample frame. Smaller systematic samples with random starts are often filtered out, limiting the risk of falling victim to periodic sampling frames. Additionally, we can comprehend the estimated variation encompassing the sample by examining the variance inside the sub-sample. 

For instance, if we have a population of N = 500 individuals and want to utilize systematic sampling to get a sample of n = 100, the population must be listed in random order. 

f = 500/100 = 20% would be the sample fraction. 

In this situation, k equals N/n = 500/100 = 5. A researcher can now select a random number between 1 and 5. 

Consider the following scenario: You choose option 2. Begin with the second unit in the list and select a sample from every kth unit (every fifth unit because k = 5). You would sample units 2, 7, 12, 17, and up to 500. 

Advantages of systematic sampling 

• It is a rapid strategy, which may save statisticians significant time. This method makes it very simple for researchers and analysts to select an appropriate sample size because it is so efficient. Almost every sample member does not need to be numbered, making it easy to represent a given population. 

• The method yields more efficient and acceptable findings compared to other statistical approaches. 

• Compared to other statistical procedures, the probabilities of data manipulation are relatively low. 

• This procedure is fairly straightforward. It is one of the primary reasons why analysts and researchers favor this methodology over all others.

• Risks associated with systematic sampling are a bare minimum. Even though the population under evaluation is very varied, this method is advantageous due to the sample’s organized distribution of members. It increases the likelihood that the data obtained during a study effort accurately reflects the complete demographic picture.

• It is user-friendly and convenient. The framework of this approach makes it easy for researchers to produce, evaluate, and conduct samples. Since the selection procedure is predetermined, the only unpredictable aspect of the task is who will be chosen first. Then, the selection process continues throughout the linear or circular pattern established until the population group selected is ready for evaluation. 

• Systematic sampling is advantageous in settings with limited funds. In cases where finances are a contributing factor to the research, this procedure is ideal. 

• Using systematic sampling, researchers can represent an entire population quickly and easily. As the goal is to obtain representative data, individual identifications are not necessary for each sample member. It facilitates rapid data creation for analysis since all that is needed to begin is to identify the target population. 

• Compared to random sampling, the samples generated by a systematic sampling method are more accurate. As soon as the initial cut has been made, researchers clearly know who will be a part of the study. Since the researchers in charge of the study can’t choose who gets their data included, there is far less room for bias. In other words, their fate is sealed once a certain population is selected. 

• In addition to preserving the high output of sampling work on massive themes with a low probability of error, it also provides a minimal danger of data tampering during data collection.

Disadvantages of Systematic Sampling 

• An issue arises when it is impossible to determine the population’s size. It even undermines the efficacy of systematic sampling in some fields, such as animal research. Since the researcher chooses the sample interval, data tampering and commercial activity are possible. 

• Sampling systems rely on accessible and quantifiable data regarding population size within a given demographic category. When that is not an option, a reasonable population estimate of the problem is needed for this strategy. Given that the size of the participant pool depends on dividing this total number, the selection method cannot proceed without it. 

• The systematic sampling procedure may be more obvious to some participants if a smaller subset of the population is being studied. Since the demographics of individuals not included in the process will differ from those who are, this disadvantage might contribute to bias. This might backfire by encouraging some respondents to submit false data in an attempt to influence the study’s findings for their own benefit.

• If randomization is of the utmost importance in the study, systematic sampling is not the ideal solution. While this technique requires less time and is easier to use than other methods of collecting data, it might have an adverse effect on the results. However, the purpose of the effort is to reduce sample error, even though the impact may not be noticeable. Due to misplaced mail or reluctant individuals, distributing questionnaires or surveys may not be a viable sample strategy. 

• In order for systematic sampling to be adequate, there must be some element of chance within the population being sampled. If the demographics follow a usual pattern, there is a high chance of picking typical situations by mistake. Thus, indicating that vital parts of the population may be excluded from the study without the researchers even realizing it.

Kultar Singh – Chief Executive Officer, Sambodhi