Stratified Random Sampling Techniques for Better Data Insights 

Are you looking for a credible method to gather data that accurately represents a larger population? Stratified random sampling might be the solution for you.  

In this piece, we’ll go into what stratified random sampling is, why it’s useful, and how to implement it so your data truly represents the population. 

Stratified Random Sampling: What Is It? 

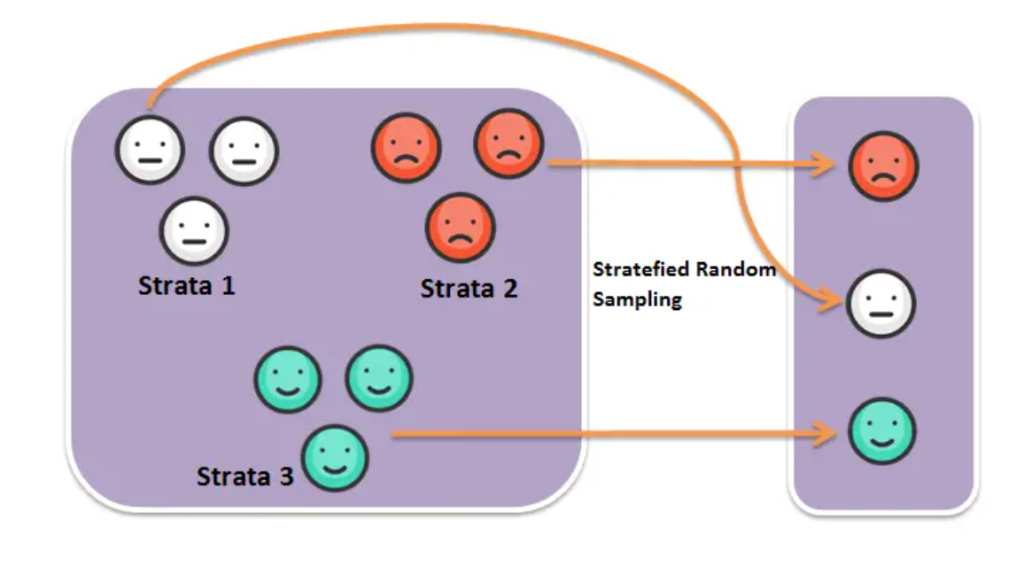
The definition of stratified random sampling is a ‘ sampling technique that divides a population into subgroups (strata) based on certain characteristics.’  

The subgroups should be homogeneous and distinct from each other. Furthermore, we randomly select a sample from each subgroup in proportion to its size in the population. 

Researchers should use this sampling to ensure the sample accurately reflects each subgroup’s population and traits. 

Importance of Stratified Random Sampling 

Stratified random sampling is essential for achieving unbiased and accurate results when studying a population with diverse characteristics. It guarantees adequate representation of each subgroup in the sample, improving the precision of estimates and reducing sampling error.  

Moreover, stratified random sampling can be cost-effective compared to other sampling techniques. It reduces the level of precision since the sample size should be proportional to each subgroup’s size in the population.  

Overall, you can save time and money by using a smaller sample size while still getting trustworthy results. 

How to Use Stratified Random Sampling 

To use stratified random sampling, follow these steps: 

1. Define the population: Determine the population you want to study, and its characteristics, then figure out the relevant subgroups based on these. 

2. Determine sample size: Determine the sample size needed for each subgroup based on the population size and desired level of precision. 

3. Randomly select samples: Use a random sampling method to select samples from each subgroup. Hence, the sample size for each subgroup should be proportional to the size of that subgroup in the population. 

4. Analyze the data: Examine the information gathered from each subgroup and compare the outcomes. 

Advantages of Stratified Sampling 

1. Increased accuracy: Stratified random sampling improves the precision of estimates by ensuring that each subgroup is well represented in the sample. 

2. Cost-effective: It is more cost-effective than other sampling approaches because it lowers the sample quantity needed to get a particular degree of precision. 

3. Comparability: Representing each subgroup in the sample makes it simpler to compare results between subgroups. 

4. Adequate representation: Each subgroup’s characteristics are adequately represented in the sample, improving the accuracy of estimates. 

Disadvantages of Stratified Sampling 

1. Increased complexity: Stratified random sampling is more complex than simple random sampling, making it more challenging to implement. 

2. Biased results: If the subgroups are not well-defined or homogeneous, the results may be biased. 

3. Time-consuming: Stratified random sampling requires more time and resources than simple random sampling, making it less feasible for some research projects. 

Examples of Stratified Sampling 

Suppose you want to study the opinions of the residents of a city on a new government policy. The city has four neighborhoods, each with different characteristics that may affect people’s opinions. To ensure that your sample accurately represents the city’s population, you can use stratified random sampling. 

First, you would divide the city into four strata based on neighborhoods. Then, you would determine the sample size required for each stratum based on its population size and the desired level of precision. Secondly, randomly choose participants from each stratum according to how big it is in the population. 

Finally, you would analyze the data collected from each stratum and compare the results across neighborhoods. This would give you a more accurate and representative view of the city’s residents’ opinions on the new policy. 

How to Calculate Sample Size in Stratified Random Sampling 

To calculate the sample size required for each stratum in stratified random sampling, you can use the following formula: 

n = (N * nh * σh²) / [(N – 1) * e² + nh * σh²] 

Where: 

n = sample size required for the stratum 

N = population size of the stratum 

nh = proportion of the stratum in the total population 

σh² = variance of the stratum 

e = desired level of precision (margin of error) 

Using this formula, you may calculate the sample size for each subgroup to get the desired results. 

Key Considerations for Sampling 

There are several important factors when utilizing stratified random sampling, including: 

Randomization: A random sampling method should be used to select participants. This helps to avoid bias and ensure an equal chance for selection from the population. 

Sample size: The sample size should be calculated based on its population size and the desired level of precision. This ensures that the sample is large enough to achieve reliable results. 

ALSO READ: Defining Snowball Sampling— Methods, Advantages, and Disadvantages 

How to Avoid Common Pitfalls in Stratified Sampling 

To ensure that your stratified random sampling is effective and unbiased, you should avoid the following: 

Poorly defined subgroups: The results may be biased if the subgroups are not well-defined or homogeneous. 

Inadequate sample size: The results may not be accurate if the sample size is too small. 

Non-random sampling: Non-random sampling methods may bias the sample. Furthermore, leading to inaccurate estimates. 

ALSO READ: Judgmental Sampling: An Effective but Less-talked Method 

Conclusion 

Stratified random sampling is a powerful tool for accurately collecting data representing a larger population. Stratified random sampling guarantees proper reflection of the features of each subgroup. For this reason, we divide the population into homogeneous subgroups. After that, choose a sample from each subgroup. 

You can obtain accurate and representative results by calculating the required sample size for each stratum and avoiding common pitfalls such as poorly defined subgroups, inadequate sample size, and non-random sampling.   

In summary, stratified random sampling is a valuable tool for collecting data that accurately represents a population. It is crucial to use this technique appropriately to obtain reliable results.