Stratified Random Sampling: A Microscopic Introduction 

Stratified random sampling, also known as proportionate random sampling, involves splitting a population into mutually exclusive and exhaustive subgroups/strata and picking a simple random sample from each subgroup/stratum.  

Subgroups can be characterized by various factors, such as gender, age, religion, and geographic region. However, it is essential to note that stratification does not exclude randomness. Moreover, it is asserted that stratified random sampling is more accurate than ordinary random sampling. Since the variation between groups within a homogeneous stratum is smaller than that of the population as a whole, this is only true if there are more homogenous strata. The confidence intervals for stratified sampling will be narrower than those for a random sample of the same population.  

In contrast, random sampling has significant advantages over stratified random sampling. Using stratified random sampling, researchers may generate unique findings for each stratum, providing crucial information about each stratum and enabling comparisons across strata.  

Use Case  

Suppose, for example, that the researchers desire to confirm that a sample of ten from 100 voters has an equal proportion of male and female voters. In this case, they must first split the population into men and women. Assuming a voter population of 60 males and 40 females.  

The sample will consist of the following proportions of men and women:  

The number of men in the sample equals (10/100) 60 = 6, whereas the number of girls equals (10/100) 40 = 4.  

Using simple or systematic random sampling, researchers can select six males and four females to refine the sample.  

Two Subtypes Of Stratified Random Sampling 

• Proportional stratified random sampling, in which each stratum receives the same sample proportion  
• Disproportionate stratified random sampling, in which each stratum receives a different sample proportion.  

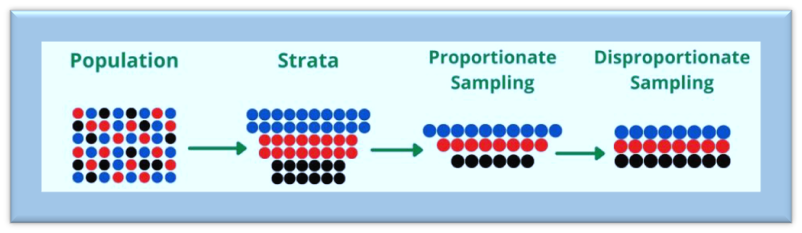
Oversampling specific subpopulations using proportionate stratified sampling can also be done to determine the exact statistics for those subpopulations apart from each other. A further justification for using a disproportional stratified sample is that certain strata have a higher unit cost than others.  

When assessing significance and confidence levels for the overall sample using uneven stratified sampling, it is essential to emphasize that instances must be weighted to restore balance. Since weighting reduces the precision of estimates from stratified sampling, disproportional stratified samples are frequently less precise than proportional stratified samples.  

Thus, the accuracy of proportional stratified sampling is equivalent to that of simple random sampling. Estimates of standard error based on stratified samples may be more or less precise than those found on simple random samples.  

When the population is diverse in the variable or trait under investigation, stratified random sampling is employed to achieve more accurate findings.  

Related: Proven Tips to Improve Quality of Research Surveys  

Advantages

• The subdivision of the population into reasonably homogenous groupings facilitates administrative efficiency. It eventually leads to cost and time savings in collecting data, interviewing respondents, and supervising fieldwork.  
   
• A stratified random sample appropriately represents each stratum or significant sector of the population. It prevents the possibility of ignoring any considerable section. Compared to other sampling strategies, it yields a more representative population sample and, thus, less variation.  
   
• As a result of the decreased variability within each stratum, stratified random sampling yields more precise estimates than basic random sampling.  
   
• Stratified random sampling is the only technique that permits us to collect findings with known precision for each stratum.  
  
• Frequently, the sampling challenges for various parts of the population vary dramatically. The issue can be efficiently addressed in such a scenario using stratified sampling.  

Disadvantages

• Disproportionate stratified sampling necessitates the assignment of weights to various strata. If the weights are incorrect, the resultant sample will not be representative and may produce biased findings.  
   
• A flawed stratification process will lead to skewed findings. No amount of sampling can eliminate the inaccuracy caused by improper stratification. The distribution of sample sizes to distinct strata necessitates a precise understanding of the population size in each stratum.  

Kultar Singh – Chief Executive Officer, Sambodhi